Fenda hiperbólica

Descrição

Este experimento é composto por uma placa na posição vertical, com duas fendas curvas, que na verdade são duas hipérboles. Embaixo da placa há uma plataforma giratória com duas hastes retas inclinadas que convergem para um vértice na parte superior. O aspecto muito curioso e não intuitivo é que ao girar a plataforma, estas hastes retas passam através das duas fendas curvas sem ao menos tocá-las. A explicação envolve a formação de superfícies de revolução. Vamos exemplificar com 3 situações de um segmento de reta girando em torno de um eixo: 1) o segmento de reta está paralelo ao eixo de rotação. Se este segmento de reta girar em torno do eixo, a superfície de revolução será um cilindro. 2) o segmento de reta está inclinado e encosta no eixo de rotação. Ao girar, o segmento de reta criará dois cones de revolução. 3) o segmento de reta está inclinado com relação ao eixo de rotação, mas sem tocá-lo. Neste caso, a superfície de revolução será um hiperbolóide, que é a superfície de nosso interesse.

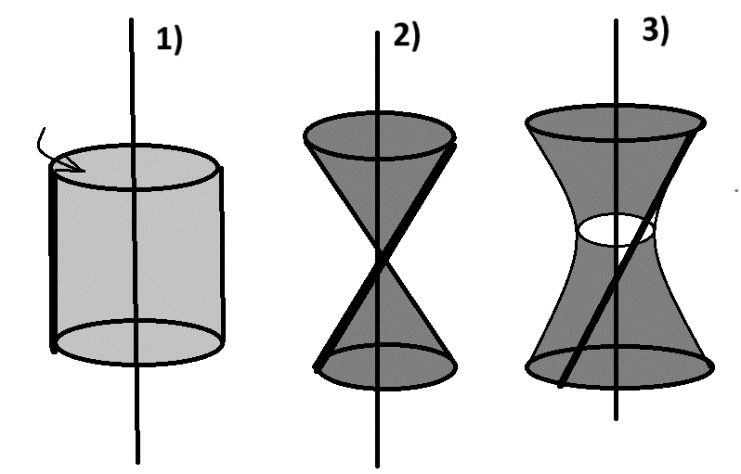
Dessa forma, podemos comprovar que uma superfície curva como um hiperbolóide pode ser gerado a partir da rotação de um segmento de reta, o que não é nada intuitivo. Na física e na engenharia existem algumas aplicações de uso dessas superfícies de revolução. Por exemplo, as chaminés das grandes usinas nucleares têm o formato de hiperbolóide. São construções muito resistentes e mais simples, pois a sua utilizam apenas de vigas metálicas retas na sua estrutura.

Conceitos e Princípios Físicos Abordados

Links Relacionados

Artigos em português:

Artigos em outros idiomas:

Vídeos em português:

Vídeos em outros idiomas:

Opções de acessibilidade

GTranslate

Laboratório de Demonstrações

Fenda hiperbólica