Looping - Azeheb

Descrição

Neste experimento uma bola de borracha é largada num trilho a uma certa altura, ℎ. Na primeira parte, o trilho é reto e inclinado fazendo com que a bola desça sobre ele com aceleração constante. Na segunda parte, o trilho tem a forma de uma hélice cujo passo é pequeno o suficiente para que a hélice possa ser aproximada por uma circunferência de raio r, contida num plano vertical, onde ℎ = 0 corresponde ao ponto inferior da circunferência (a base do “loop”). Repetindo o experimento várias vezes, para diferentes alturas, nota-se que só a partir de uma certa altura, ℎ ≥ 𝐻, a bola se move por todo o trilho sem perder o contato com ele, mesmo quando está debaixo do trilho, “de ponta-cabeça” no topo do “loop” (trecho circular).

Para entender a relação entre H e r, precisamos notar que quando a bola se move ao longo do trilho, apenas duas forças são relevantes no seu movimento, a força normal, , do trilho sobre a bola e a força peso (gravitacional, ). Precisamos, também, lembrar dos conceitos de Movimento Circular Uniforme e de Conservação da Energia:

Movimento Circular Uniforme (MCU): O movimento da bola ao longo do “loop” é circular, mas não é uniforme. Porém, no topo do “loop” a força resultante (normal mais gravitacional) é centrípeta, não tem componente tangencial, de modo que a derivada do módulo da velocidade é zero:

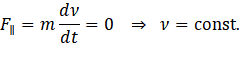
Ou seja, no topo do “loop”, por um instante, o módulo da velocidade é constante (para de diminuir para começar a aumentar). Neste ponto e por um instante, o movimento pode ser considerado um MCU:

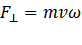
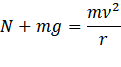
Com 𝜔 = 𝑣/𝑟 sendo a velocidade angular do MCU. (Em geral, 𝜔 é a taxa de variação da direção de

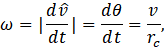
sendo o raio de curvatura da trajetória da partícula e o ângulo entre e que no MCU coincide com o ângulo entre e .)

Como 𝑁 ≥ 0:

Sendo 𝑣_min o menor valor da magnitude da velocidade da bola no topo do “loop”, para a qual temos nesse ponto, um MCU (aquela para a qual a força centrípeta é mínima, ou seja, quando a magnitude da força normal se anula e a força centrípeta é apenas a força gravitacional. É o menor valor da magnitude da velocidade, no topo do “loop”, para que a bola se mova por todo o trilho sem perder o contato com ele.

Conservação da energia: O trabalho realizado pela força normal é sempre zero, por ser esta força perpendicular à velocidade. Assim, pelo teorema do trabalho e da energia cinética (𝑊 = Δ𝐾), a força normal não altera a energia cinética da bola. A força gravitacional é conservativa, o trabalho realizado por ela pode ser contabilizado como uma variação da energia potencial gravitacional (𝑊𝑔 = −Δ𝑈𝑔), de modo que a energia mecânica, a soma da energia potencial gravitacional mais a energia cinética (𝐸m = 𝑈g + 𝐾), permanece constante. Assim, a velocidade mínima da bola no topo do “loop” (ℎ = 2𝑟) depende da altura inicial (ℎ = 𝐻)

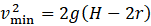
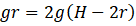
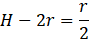
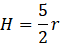
Conclusão: Para que a bola se mova por todo o trilho sem perder o contato com ele, ela deve ser abandonada sobre o trilho a uma altura que está metade do raio do “loop” acima do topo do “loop” ( 5/2 𝑟 acima da base do “loop”).

Conceitos e Princípios Físicos Abordados

Aborda conceitos físicos de energia cinética, energia potencial gravitacional, transformação, conservação e dissipação de energia e forças dissipativas.

Material Utilizado

Equipamento industrializado, comercializado pela Azeheb <https://azeheb.com.br>.

Links Relacionados

Artigos em português:

Artigos em outros idiomas:

Vídeos em português:

Vídeos em outros idiomas:

Opções de acessibilidade

Laboratório de Demonstrações

Looping - Azeheb